1. 正则化
它可以改善或者减少过度拟合问题
2. 欠拟合(模型的高偏差)
欠拟合是指模型拟合程度不高,数据距离拟合曲线较远,或者模型没有很好地捕捉到数据特征,不能够很好地拟合数据。
3. 过拟合(模型的高方差)
为什么出现过拟合
- 特征过多
- 训练集数据较少
- 模型复杂
对过拟合的理解
如果我们拟合一个高阶多项式,那么这个函数能很好的拟合训练集能拟合几乎所有的训练数据,这就面临可能函数太过庞大的问题,即变量太多。同时如果我们没有足够的数据去约束这个变量过多的模型,就会出现过度拟合的情况。虽然训练出的模型能够很好的拟合训练集的样本数据,但很有可能无法泛化新样本。
如何解决过拟合
4. 怎么应用正则化
思想与做法
修改代价函数,从而收缩(惩罚)所有的参数值,因为我们并不知道具体的去收缩(惩罚)哪些参数,
修改后的代价函数如下:
$$
J\left(\theta\right)=\frac{1}{2m}[\sum\limits_{i=1}^{m}{({h_\theta}({x}^{(i)})-{y}^{(i)})^{2}+\lambda \sum\limits_{j=1}^{n}\theta_{j}^{2}]}
$$
$\lambda $又称为正则化参数(Regularization Parameter),它能够平衡代价函数,使$\theta_j$尽可能的小。
注:根据惯例,我们的$j$是从1开始的,也就是我们不对${\theta_{0}}$ 进行惩罚。
举一个例子
我们看这个假设函数: $h_\theta\left( x \right)=\theta_{0}+\theta_{1}x_{1}+\theta_{2}x_{2}^2+\theta_{3}x_{3}^3+\theta_{4}x_{4}^4$ 。通常地,正是那些高次项导致了过拟合的产生,所以如果我们能让这些高次项的系数接近于0的话,我们就能很好的拟合了。于是我们将修改代价函数,在其中${\theta_{3}}$和${\theta_{4}}$ 设置一点惩罚。这样做的话,我们在尝试最小化代价时也需要将这个惩罚纳入考虑中,并最终导致选择较小一些的${\theta_{3}}$和${\theta_{4}}$。修改后如下 :
$$
\underset{\theta}{\mathop\min }\,\frac{1}{2m}[\sum\limits_{i=1}^{m}{\left({h}_{\theta }\left( {x}^{(i)} \right)-{y}^{(i)} \right)^{2}+1000\theta _{3}^{2}+10000\theta _{4}^{2}]}
$$
但是正是因为我们并不知道具体的哪一个$\theta$是高次项,因此我们只能去收缩(惩罚)所有参数。
但是
如果我们令 $\lambda$ 的值很大的话,那么$\theta $(不包括${\theta_{0}}$)都会趋近于0,这样我们所得到的只能是一条平行于$x$轴的直线。所以对于正则化,我们要取一个合理的 $\lambda$ 的值,这样才能更好的应用正则化。
5. 正则化线性回归
正则化代价函数
$$
J\left(\theta\right)=\frac{1}{2m}\sum\limits_{i=1}^{m}{[(({h_\theta}({x}^{(i)})-{y}^{(i)})}^{2}+\lambda \sum\limits_{j=1}^{n}{\theta _{j}^{2})]}
$$
正则化梯度下降
要使梯度下降法令正则化后的线性回归代价函数最小化,因为我们没有对$\theta_0$进行正则化,所以梯度下降算法有两种情形:
$$
{\theta_0}:={\theta_0}-a\frac{1}{m}\sum\limits_{i=1}^{m}(({h_\theta}({x}^{(i)})-{y}^{(i)})x_{0}^{(i)})
$$
$$
{\theta_j}:={\theta_j}-a[\frac{1}{m}\sum\limits_{i=1}^{m}({h_\theta}({x}^{(i)})-{y}^{(i)})x_{j}^{\left(i\right)}+\frac{\lambda }{m}{\theta_j}]
$$
对第二个式子进行变化后,可得:
$$
{\theta_j}:={\theta_j}(1-a\frac{\lambda }{m})-a\frac{1}{m}\sum\limits_{i=1}^{m}({h_\theta}({x}^{(i)})-{y}^{(i)})x_{j}^{\left(i\right)}
$$
可以看出,正则化线性回归的梯度下降算法的变化在于,每次都在原有算法更新规则的基础上令$\theta $值减少了一个额外的值。
PS:梯度下降仍然是对$J(\theta)$进行最小化,通过求导,得出梯度下降算法
正则化正规方程
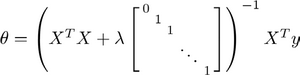
注:图中的矩阵尺寸为 $(n+1)*(n+1)$。
值得一提的是,哪怕此时$X$不可逆,经过$\lambda$相加变化后的矩阵将是可逆的。
6. 正则化逻辑回归
正则化代价函数
$$
J\left(\theta\right)=\frac{1}{m}\sum\limits_{i=1}^{m}{[-{y}^{(i)}\log \left({h_\theta}\left({x}^{(i)}\right)\right)-\left(1-{y}^{(i)} \right)\log\left(1-{h_\theta}\left({x}^{(i)}\right) \right)]}+\frac{\lambda}{2m}\sum\limits_{j=1}^{n}\theta _{j}^{2}
$$
ps:注意这里$\lambda$的仍为$\frac{1}{2m}$
正则化梯度下降
类似地,因为我们没有对$\theta_0$进行正则化,所以梯度下降算法有两种情形:
$$
{\theta_0}:={\theta_0}-a\frac{1}{m}\sum\limits_{i=1}^{m}(({h_\theta}({x}^{(i)})-{y}^{(i)})x_{0}^{(i)})
$$
$$
{\theta_j}:={\theta_j}-a[\frac{1}{m}\sum\limits_{i=1}^{m}({h_\theta}({x}^{(i)})-{y}^{(i)})x_{j}^{\left( i \right)}+\frac{\lambda }{m}{\theta_j}]
$$
看起来和线性回归的一模一样,实际上我们知道这里 ${h_\theta}\left( x \right)=g\left( {\theta^T}X \right)$,所以与线性回归不同。
PS:值得注意的是,${\theta_{0}}$仍然不参与其中的任何一个正则化。
注:
泛化能力(generalization ability)
泛化能力是指机器学习算法对新鲜样本的适应能力。学习的目的是学到隐含在数据背后的规律,对具有同一规律的学习集以外的数据,经过训练的模型也能给出合适的输出,该能力称为泛化能力。

