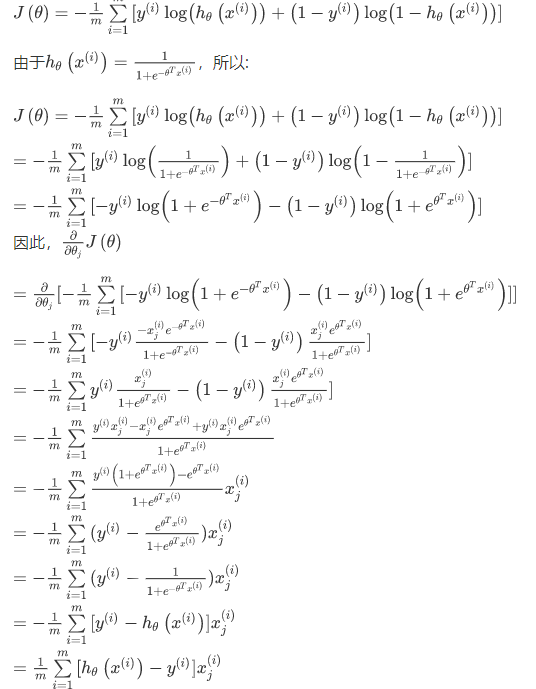机器学习-逻辑回归

什么是逻辑回归

逻辑回归算法是分类算法，可能它的名字里出现了“回归”让我们以为它属于回归问题，但逻辑回归算法实际上是一种分类算法，它主要处理当 $y$ 取值离散的情况，如：1 0 。

为什么不使用线性回归算法处理分类问题

假设我们遇到的问题为二分类问题，那么我们可能将结果分为负向类和正向类，即$y\in0,1$ ，其中 0 表示负向类，1 表示正向类。如果我们使用线性回归，那么假设函数的输出值可能远大于 1，或者远小于0，但是我们需要的假设函数输出值需要在0到 1 之间，因此我们需要用到逻辑回归算法。

逻辑回归的假设函数与理解

逻辑回归的假设函数 sigmoid function 表示方法 :

$$
h_\theta(x) = \frac{1}{1+e^{-\theta^Tx}}
$$

理解记忆:

其实里面的$\theta_Tx$就是线性回归时的假设函数 h(x) ，
$$
h(x) = \theta^Tx = \sum_{j=0}^{n}{\theta_jx_j}
$$
而逻辑回归的假设函数其实就是将线性回归的表达式 h(x) 以 z 的形式代入到了 S 型函数(sigmoid function) 中 :
$$
g(h(x)) = g(z) = \frac{1}{1+e^{-z}}
$$
ps: 这里我们用$h(x)$表示的是线性回归的假设函数，之后的$h$都将表示逻辑回归的假设函数。值得一提的是S型函数和我们的假设函数没关系，它只是一个输出值在0~1之间的函数，仅此而已。我们做的只是把之前得到的线性回归假设函数给代入进去形成逻辑回归的假设函数，这样

对假设函数的解释 :

给定 x ，根据选择的参数计算出y = 1 的概率，具体的概率公式如下 :
$$
h_\theta(x) = P(y=1|x; \theta)
$$

Sigmoid - Python:

import numpy as np

def sigmoid(z):
    return 1 / (1 + np.exp(-z))

判定边界(decision boundary)

如何得出判定边界 :

在逻辑回归的假设函数中，但凡输出结果 $h_\theta(x)$大于 0.5 的，我们都将预测结果 $y$ 收敛于 1 ；小于 0.5 的，收敛于 0 ；而恰好等于 0.5 的，收敛1 或 0 都可以，我们可以自己设定它如何收敛。由此，我们的输出值就都在 0 到 1 之间了。而当 $h_\theta(x)$ 大于 0.5 时，$\theta^Tx$ 大于 0.5， $h_\theta(x)$ 小于 0.5 时，$\theta^Tx$ 小于 0.5， $h_\theta(x)$ 等于 0.5 时，$\theta^Tx$ 等于 0.5。
当然，具体的阈值是可以调整的，比如说你是一个比较保守的人，可能将阈值设为 0.9 ，也就是说有超过 90% 的把握，才相信这个$y$收敛于 1 。

由此，我们能够绘制出判定边界 :
$$
\theta^Tx = 0
$$

关于判定边界 :

决策边界不是训练集的属性，而是假设本身及其参数的属性
只要给出确定的参数$\theta$，就确定了我们的决策边界
高阶多项式(多个特征变量)能够让我们得到更复杂的决策边界

逻辑回归的代价函数，梯度下降自动拟合$\theta$，以及代价函数的推导过程

逻辑回归的代价函数 :

$$
J(\theta) = \frac{1}{m}\sum_{i=1}^{m}Cost(h_\theta(x^{(i)}),y^{(i)})
$$
其中$Cost$ :
$$
Cost(h_\theta(x),y) = -ylog(h_\theta(x)) - (1-y)log(1-h_\theta(x))
$$
因此$J(\theta)$ :
$$
J(\theta) =-\frac{1}{m}[\sum_{i=1}^{m} y^{(i)}log(h_\theta(x^{(i)})) + (1-y^{(i)})log(1-h_\theta(x^{(i)}))]
$$

使用对数几率的原因:

代价函数 $J(\theta)$ 会是一个凸函数，并且没有局部最优值。否则我们的代价函数将是一个非凸函数。

逻辑回归的梯度下降算法 :

Repeat {
$$
\theta_j := \theta_j - \alpha \frac{\partial}{\partial\theta_j} J(\theta)
$$
(simultaneously update all )
}

求导后得到：

Repeat {
$$
\theta_j := \theta_j - \alpha\sum_{i=1}^{m}(h_\theta(x^{(i)})-y^{(i)})x_j^{(i)}
$$
(simultaneously update all )
}

ps : 逻辑回归梯度下降结果与线性回归梯度下降结果一致，但其中的$h_\theta(x)$并不一样，因此本质上是不同的。

关于特征缩放和均值归一化:

思想:

在有多个特征的情况下，如果你能确保这些不同的特征都处在一个相近的范围，这样梯度下降法就能更快地收敛。使代价函数$J(θ)$的轮廓图的形状就会变得更圆一些。

做法:

一般地，我们执行特征缩放时，我们通常将特征的取值约束到接近−1到+1的范围。其中，特征x0总是等于1，因此这已经是在这个范围内了，但对于其他的特征，我们需要通过除以不同的数来让它们处于同一范围内。除了在特征缩放中将特征除以最大值以外，有时候我们也会进行一个称为均值归一化的操作:
$$
x_n = \frac{x_n-μ_n}{s_n}
$$
其中，$μ_n$是平均值，$s_n$是标准差

好处:

更好的进行梯度下降，提高代价函数的收敛速度
提高代价函数求解的精度
更适合解决大型机器学习的问题

其他相较于梯度下降算法更好的的令代价函数最小的算法(高级优化[超纲])

常用算法:

共轭梯度(Conjugate Gradient)
局部优化法(BFGS - Broyden fletcher goldfarb shann)
有限内存局部优化法(LBFGS)

好处:

这些算法内部有一个智能的内部循环(线性搜索算法)，能够尝试不同的 $\alpha$ 并自动的选择一个好的学习速率 $\alpha$ ，这样就不需要手动选择 $\alpha$
收敛速度通常比梯度下降算法更快速

缺点:

比梯度下降算法更加复杂

使用逻辑回归算法解决多类别问题

思想:

将多分类问题拆分成多个二分类问题并得出多个模型。最后，在我们需要做预测时，我们将所有的分类机都运行一遍，然后对每一个输入变量，都选择最高可能性的输出变量。

做法:

我们将多个类中的一个类标记为正向类（$y=1$），然后将其他所有类都标记为负向类，这个模型记作$h_\theta^{\left( 1 \right)}\left( x \right)$。接着，类似地我们选择另一个类标记为正向类（$y=2$），再将其它类都标记为负向类，将这个模型记作 $h_\theta^{\left( 2 \right)}\left( x \right)$,依此类推。
最后我们得到一系列的模型简记为： $h_\theta^{\left( i \right)}\left( x \right)=p\left( y=i|x;\theta \right)$其中：$i=\left( 1,2,3….k \right)$ 。
然后我们将这多个逻辑回归分类器进行训练并得出最终模型：$h_\theta^{\left( i \right)}\left( x \right)$，其中 $i$ 对应每一个可能的 $y=i$，最后，当我们需要进行预测时，输入一个新的 $x$ 值，我们要做的就是在这多个分类器里面输入 $x$，然后在多个分类器得出的结果中，选出一个最大的$ i$，即$\mathop{\max}\limits_i\,h_\theta^{\left( i \right)}\left( x \right)$。

逻辑回归梯度下降中代价函数求导过程

1540643022637